General Word Problems

General Strategy

Recall the general strategy for setting up word problems. Refer to the Problem Solving Strategies page for more detail.

1. Read the problem carefully: Determine what is known, what is unknown, and what question is being asked.
2. Represent unknown quantities in terms of a variable.
3. Use diagrams where appropriate.
4. Find formulas or mathematical relationships between the knowns and the unknowns.
5. Solve the equations for the unknowns.
6. Check answers to see if they are reasonable.

Number/Geometry Problems

Example:  Find a number such that 5 more than one-half the number is three times the number.

Let x be the unknown number.
Translating into math:	5 + x/2 = 3x
Solving: (First multiply by 2 to clear the fraction)	5 + x/2 = 3x 10 + x = 6x 10 = 5x x = 2

Example: If the perimeter of a rectangle is 10 inches, and one side is one inch longer than the other, how long are the sides?

Let one side be x and the other side be x + 1.

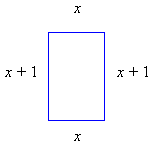
Then the given condition may be expressed as

x + x + (x + 1) + (x + 1) = 10

Solving:

4x + 2 = 10
4x = 8
x = 2

so the sides have length 2 and 3.

Rate-Time Problems

• Rate = Quantity/Time

or

• Quantity = Rate × Time

Example:  A fast employee can assemble 7 radios in an hour, and another slower employee can only assemble 5 radios per hour. If both employees work together, how long will it take to assemble 26 radios?

The two together will build 7 + 5 = 12 radios in an hour, so their combined rate is 12 radios/hr.

Using Time = Quantity/Rate, Time = 26/12 = 2 1/6 h or 2 hours 10 minutes

Example:  you are driving along at 55 mph when you are passed by a car doing 85 mph. How long will it take for the car that passed you to be one mile ahead of you?

We know the two rates, and we know that the difference between the two distances traveled will be one mile, but we don’t know the actual distances. Let D be the distance that you travel in time t, and D + 1 be the distance that the other car traveled in time t. Using the rate equation in the form distance = speed • time for each car we can write

D = 55 t, and D + 1 = 85 t

Substituting the first equation into the second,

55t + 1 = 85t –30t = –1
t = 1/30 hr(or 2 minutes)

Mixture Problems

Example:  How much of a 10% vinegar solution should be added to 2 cups of a 30% vinegar solution to make a 20% solution?

Let x be the unknown amount of 10% solution. Write an equation for the amount of vinegar in each mixture:

(amount of vinegar in first solution) + (amount of vinegar in second solution) = (amount of vinegar in total solution)

0.1x + 0.3(2) = 0.2(x + 2)

0.1x + 0.6 = 0.2x + 0.4

–0.1x = –0.2

x = 2 cups

Troubled by “General Word Problems” in your math course? Secure expert assignment help to solve them with ease and confidence!