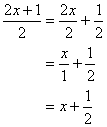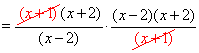Canceling Like Factors
When we reduce a common fraction such as
![]()
we do so by noticing that there is a factor common to both the numerator and the denominator (a factor of 2 in this example), which we can divide out of both the numerator and the denominator.
![]()
We use exactly the same procedure to reduce rational expressions.
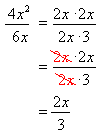
Polynomial / Monomial
Each term in the numerator must have a factor that cancels a common factor in the denominator.
![]()
but
![]()
cannot be reduced because the 2 is not a common factor of the entire numerator.
WARNING You can only cancel a factor of the entire numerator with a factor of the entire denominator
| However, as an alternative, a fraction with more than one term in the numerator can be split up into separate fractions with each term over the same denominator; then each separate fraction can bereduced if possible:
· Think of this as the reverse of adding fractions over a common denominator. Sometimes this is a useful thing to do, depending on the circumstances.You end up with simpler fractions, but the price you pay is that you have more fractions than you started with. |
- Polynomials must be factored first. You can’t cancel factors unless you can see the factors:
Example:

- Notice how canceling the (x– 2) from the denominator left behind a factor of 1
Multiplication and Division
Same rules as for rational numbers!
Multiplication
- Both the numerators and the denominators multiply together
- Common factors may be cancelled before multiplying
Example:
| Given Equation: |
|
| First factor all the expressions: (I also put the denominators in parentheses because then it is easier t see them as distinct factors) |
|
| Now cancel common factors—any factor on the top can cancel with any factor on the bottom:
|
|
| Now just multiply what’s left. You usually do not have to multiply outthe factors, just leave them as shown. |
Division
- Multiply by the reciprocal of the divisor
- Invert the second fraction, then proceed with multiplication as above
- Do not attempt to cancel factors before it is written as a multiplication
Addition and Subtraction
Same procedure as for rational numbers!
- Only the numerators can be addedtogether, and only when all the denominators are the same
Finding the LCD
- The LCD is built up of all the factors of the individual denominators, each factor included the most number of times it appears in an individual denominator.
- The product of all the denominators is always a commondenominator, but not necessarily the LCD (the final answer may have to be reduced).
Example:
| Given equation: |
|
| Factor both denominators: |
|
| Assemble the LCD: Note that the LCD contains bothdenominators |
|
| Build up the fractions so that they both have the LCD for a denominator: (keep both denominators in factored form to make it easier to see what factors they need to look like the LCD) |
|
| Now that they are over the same denominator, you can add the numerators: |
|
| And simplify:
|
Confused by Simplifying Rational Expressions in math? Get professional assignment help to clarify your understanding and excel!
If you need someone to do your math homework , you can turn to CWassignments.com. Our experts can help you with all kinds of STEM assignments including ‘do my programming homework‘ help.