Introduction
Binary tree are a fundamental and useful type of data structure. A binary tree’s diameter, which reflects the distance between any two nodes in the tree, is an important feature. This article will go into great detail on how to use Python to calculate the diameter of the binary tree. We will go over recursive and iterative methods, including step-by-step instructions, in-depth justifications, and copious samples of code.
What is a Binary Tree?
Let’s explore the definition of a binary tree and its many elements in more detail before moving on to the computation of the diameter of the binary tree. Each node in a binary tree has a maximum of two children: a left child and a right child. Nodes without any offspring are referred to as leaf nodes, while the topmost node is known as the root.
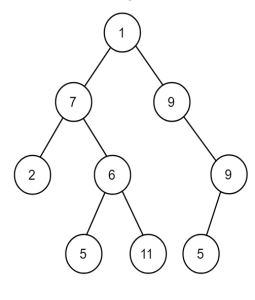
By calculating the heights of the left and right subtrees for each node and combining them to determine the diameter, the recursive method takes use of this relationship. Let’s explore the recursive method in greater detail.
Recursive Approach
The divide-and-conquer tactic is utilized in the elegant and simple recursive technique. It includes calculating the left and right subtree heights for each node and taking three instances into account for the diameter:
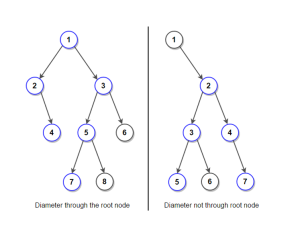
a) The diameter passes through the root node, and its length is the sum of the heights of the left and right subtrees plus one (for the root node).
b) The diameter lies entirely in the left subtree.
c) The diameter lies entirely in the right subtree.
Let’s implement the recursive function to calculate the diameter:
class TreeNode:
def __init__(self, val): self.val val
self.left = None
self.right None
#Create a binary tree
# 1
# / \
# 2 3
# /\
# 4 5
root = TreeNode(1)
root root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right TreeNode(5)
We created a simple binary tree with five nodes in the example. The root node has two children – nodes with values 2 and 3, respectively. The left child of the root node (with value 2) has its children – nodes with values 4 and 5, respectively.
Calculating the Diameter of the Binary Tree
We must determine the longest path between any two tree nodes in order to determine the binary tree’s diameter. The root may or may not be crossed by this path. Let’s examine the idea of diameter in more detail and see how it relates to the sizes of the tree’s subtrees.
- A binary tree’s diameter is the highest of the following three values:
- The diameter of the left subtree.
- The diameter of the right subtree.
- The longest path between leaves passes through the root.
By calculating the heights of the left and right subtrees for each node and combining them to determine the diameter, the recursive method takes use of this relationship. Let’s explore the recursive method in greater detail.
Recursive Approach
The divide-and-conquer tactic is utilized in the elegant and simple recursive technique. It includes calculating the left and right subtree heights for each node and taking three instances into account for the diameter:
a) The diameter passes through the root node, and its length is the sum of the heights of the left and right subtrees plus one (for the root node).
b) The diameter lies entirely in the left subtree.
c) The diameter lies entirely in the right subtree.
Let’s implement the recursive function to calculate the diameter:
class TreeNode:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
#Python function to calculate the height of a binary tree def
def height(node):
if node is None:
return 0
return max (height(node.left), height(node.right)) + 1
#Python function to calculate the diameter
def diameter (node):
if node is None:
return 0
#Calculate the height of the left and right subtrees
left_height = height(node.left)
right_height = height(node.right)
#Calculate the diameter in the left and right subtrees
left_diameter = diameter(node.left)
right_diameter = diameter(node.right)
#Return the maximum of the three diameters
return max(left_height + right_height, max (left_diameter, right_diameter))
Example usage
# Create the binary tree root = TreeNode(1) root.left = TreeNode(2) root.right = TreeNode (3) root.left.left = TreeNode(4) root.left.right = TreeNode(5)
To calculate the diameter of this tree using our diameter function:
#Calculate and print diameter
d = diameter(root)
print("Diameter of the binary tree:", d)
Ouput:
Diameter of the binary tree: 3
In the above example, the longest path between any two nodes in the binary tree is the path from node with value 4 to node with value 3, passing through the root with value 1. The diameter of the binary tree is 4.
Iterative Approach
By using a stack or a queue to traverse the binary tree and maintain track of the diameter, the iterative technique uses an alternative strategy. This method eliminates the need for recursion and may be better in some circumstances. Utilizing a queue, we may execute the iterative strategy and traverse the binary tree in level-order. As we traverse, we can alter the diameter as we come across new nodes.
Let’s implement the iterative function to calculate the diameter:
#Python function to calculate the diameter of a binary tree iterativ
def diameter_iterative(root):
#Check for an empty tree
if root is None:
return 0
#Initialize a queue for level-order traversal
queue = []
queue.append(root)
diameter = 0
#Perform BFS to find the diameter
while queue:
node = queue.pop (0)
left_height = height(node. left)
right_height = height(node. right)
diameter = max(diameter, left_height + right_height)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return diameter
Example Usage (Consider the same binary tree as before):
# Calculate and print the diameter
d = diameter_iterative(root)
print("Diameter of the binary tree:", d)
Output
Diameter of the binary tree: 3
In the above example, the iterative approach produces the same result as the recursive approach. The iterative algorithm performs a level-order traversal of the binary tree and updates the diameter of the binary tree accordingly, ultimately finding the longest path between any two nodes in the tree.
Comparing the Recursive and Iterative Approaches
Both the recursive and iterative approaches yield the same result for calculating the diameter of the binary tree. However, they use different strategies to achieve the same goal. Let’s compare their strengths and weaknesses to better understand which approach might be more suitable for specific scenarios.
Recursive Approach
– Strengths:
– Intuitive and easy to implement for many developers.
– Elegantly leverages the divide-and-conquer strategy.
– Weaknesses:
– May encounter a stack overflow for large trees due to the recursive nature, potentially leading to performance issues.
– Extra function call overhead might affect performance.
Iterative Approach
– Strengths:
– Eliminates the risk of stack overflow for large trees, making it more efficient for large binary trees.
– No additional function call overhead, reducing memory usage.
– Weaknesses:
– Slightly more complex to implement using a queue for level-order traversal.
In general, for relatively small binary trees or when recursion is not a concern, the recursive approach is a straightforward and elegant solution. However, if you are working with large binary trees or concerned about stack overflow issues, the iterative approach provides a more efficient alternative.
Find the Diameter of a Rooted Binary Tree
One of the primary advantages of using rooted binary trees is their natural representation of hierarchical structures. This characteristic makes them ideal for modeling various real-world scenarios, such as organizational hierarchies, file systems, and network topologies. To find the diameter of a rooted binary tree, we can employ both recursive and iterative approaches. The recursive approach is based on the concept of divide-and-conquer, where we calculate the diameters of left and right subtrees for each node and combine them to find the diameter passing through the root. On the other hand, the iterative approach uses a queue or stack to traverse the tree efficiently, updating the diameter as we encounter each node.
Real-world Applications
The diameter of a binary tree is not just an abstract concept; it has practical applications in various areas of computer science and programming. Let’s explore how the diameter calculation is utilized in real-world scenarios:
1. Search Algorithms: The diameter of a binary tree is crucial in various search algorithms. For example, when implementing breadth-first search (BFS) or depth-first search (DFS) on a binary tree, the diameter can help determine the level at which the search should stop, optimizing the search process.
2. Graph Traversal: Binary trees can be considered as a special case of graphs, and finding the diameter can provide insights into the overall structure of the graph. The diameter is used to measure the efficiency of graph traversal algorithms.
3. Network Analysis: In networking and communication systems, binary trees are often used to model network structures. Understanding the diameter of such structures can help in optimizing data routing and minimizing communication delays.
Conclusion
Calculating the diameter of a binary tree is a fundamental problem in computer science and programming. Understanding this concept is essential for various search algorithms, coding assignments, and real-world applications. In this article, we explored the anatomy of a binary tree, different approaches for calculating the diameter, their respective strengths and weaknesses, and real-world use cases.
If you’re a student facing challenges with your Python homework, understanding binary trees, or calculating their diameter, and other concepts you can get exceptional do my coding services at CW Assignments. By following the approaches explained here, you can confidently tackle your Python assignments and improve your programming skills. Happy coding!









