In the realm of computer science, binary trees serve as foundational data structures, offering versatility in organizing hierarchical data. A binary tree, a specialized structure, features nodes holding data and up to two child nodes, enhancing efficiency in various tasks, including coding homework help. Nodes are pivotal to the binary tree, forming its core and function. Parent nodes connect to children nodes, creating a hierarchy. The highest node, or “root,” anchors the structure, while parents branch into left and right children, fostering organized arrangement. The tree culminates in leaf nodes, representing branch terminations. This design ensures efficient data traversal and manipulation, benefiting coding homework help tasks across computational contexts.
To visualize the notion of binary tree height, consider a simple illustration:
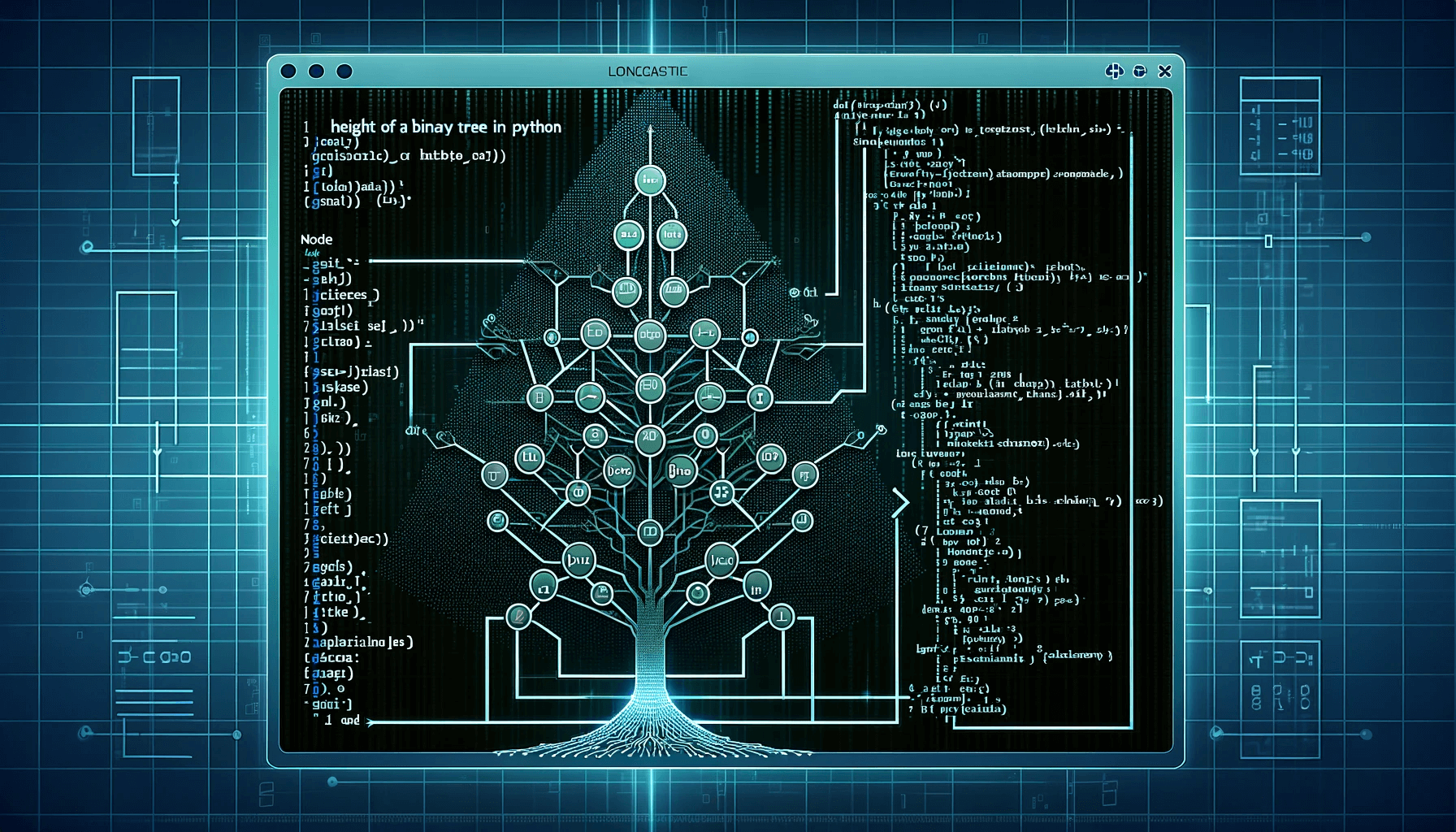
What is a Binary Tree?
A binary tree is a specialized tree structure where each element, referred to as a ‘node,’ holds specific data elements and can have up to two child nodes. Each node holds data and pointers to left and right child nodes. The root node defines the hierarchy, while leaf nodes denote branch ends. Parent nodes hold children nodes, classified by position. Binary trees efficiently manage data in storage, search, and sorting tasks, making them versatile tools in computation, including python assignment helper.
Below is a representation of a binary tree
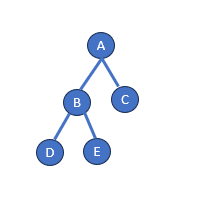
In this above numeric binary tree, the root node is 5. The left child of 5 is node 7, and the right child is node 9. Node 7 has two children: node 12 (left child) and node 15 (right child). This arrangement adheres to the hierarchical structure typical of binary trees, where nodes are organized based on their values.
The height of this binary tree is 3, as the longest path from the root node 5 to a leaf node (e.g., 5 -> 7 -> 12) encompasses three edges. Binary trees with ascending numerical values offer efficient ways to store, search, and sort data in various computer science applications.
What is the Height of a Binary Tree?
The height of a binary tree, often referred to as its depth, is quantified by the number of edges traversed from the root node to any of its leaf nodes. This measure holds significant importance in understanding the structure and balance of the binary tree. Calculating the height involves leveraging the count of nodes within the tree. Let’s denote ‘h’ as the height of the binary tree and ‘n’ as its node count.
Mathematically, the formula for calculating the height of a full binary tree is expressed as h = log2(n + 1) – 1. It’s important to note that this formula assumes the binary tree is full, signifying that each level is entirely populated, except for the final level, which is occupied from left to right. To illustrate the practical application of this formula, consider a binary tree with a solitary node, resulting in a height of 0, as validated by the equation h = log2(1 + 1) – 1 = 0. Similarly, a binary tree hosting three nodes would yield a height of 1: h = log2(3 + 1) – 1 = 1.
The formula extends its utility to binary trees with seven nodes, yielding a height of 2, and to those with fifteen nodes, exhibiting a height of 3, and so forth. While the formula offers an upper bound for the height, it’s essential to acknowledge that the actual height of a binary tree might be lower if it deviates from the characteristics of a full binary tree. In such cases, different approaches might be employed to calculate the height.
How to Find the Height of a Binary Tree
Determining the height of a binary tree involves a profound understanding of its structure and the paths that connect its nodes, crucial for various computational tasks such as python assignment helper. Let’s explore this concept using an example. Imagine a binary tree illustrated as follows:
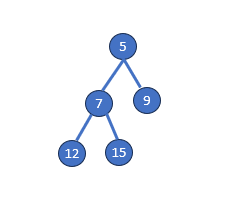
In this illustration, we’ll uncover the process of calculating the height of the binary tree. As we’ve established, the height of a binary tree corresponds to the longest path between the root node and any leaf node. Beginning from the root node, we’ll traverse through the possible paths to the leaf nodes: 10, 22, and 35. By counting the edges along these paths, we can discern the heights of the corresponding subtrees.
For the leaf nodes 10 and 22, the paths consist of three edges, resulting in a height of 3 for each. The leaf node 35, however, requires four edges to reach, indicating a height of 4. By evaluating these individual heights, we identify the maximum value (4) as the measure of the longest distance from the root node to any leaf node in this binary tree. As a result, the binary tree height is 4.
This example underscores the significance of the height metric, which captures the utmost number of edges traversed from the root to a leaf node. When a target node lacks child nodes, its height is naturally 0. This understanding of height illuminates the binary tree’s structure and facilitates the optimization of algorithms for data manipulation and retrieval. Additionally, the concept of “depth” in a binary tree corresponds to the total number of edges traversed from the root node to a specific destination node, enhancing our comprehension of the intricate relationships within the tree’s hierarchical framework.
Exploring Height with Recursion (Depth First Search)
To illustrate the calculation of the height using recursion and depth-first search, let’s consider a binary tree of height 4 with the following structure:
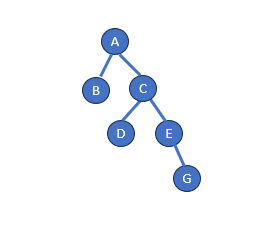
Step 1: Initiating the Inquiry
We initiate the process by inquiring the root node A about its height.
Checking the root node A:
• Node A inquires its left child B.
• Node A inquires its right child C.
Step 2: Recursive Exploration
We proceed to explore the subtrees rooted at B and C.
Applying recursion on Node B (Left Child of A):
• Node B reports its result, which is 0 (no more child nodes).
Applying recursion on Node C (Right Child of A):
• Node C inquires its left child D.
• Node C inquires its right child E.
Step 3: Investigating Leaf Nodes
Continuing the exploration, we reach the leaf nodes D and G. Let’s calculate the number of nodes along the edges from the root for each of these leaf nodes:
Applying recursion on Node D (Left Child of C):
• Node D reports its result, which is 0 (no more child nodes).
Applying recursion on Node E (Right Child of C):
• Node E inquires its left child (null).
• Node E inquires its right child G.
Applying recursion on Node G (Right Child of E):
• Node G reports its result, which is 0 (no more child nodes).
Step 4: Height Computation and Aggregation
Node E aggregates the heights from its right child G:
• Node E (Right Child of C) calculates its height:
• Height of Node G = 0 + 1 = 1
• Height of Node E = 1 + 1 = 2
• Total height = 1 + 2 = 3
Step 5: Root Node A’s Height Calculation
With insights from both subtrees, the root node A computes its height:
Calculating the height of the binary tree rooted at A:
• Max(Height of B, Height of G) = Max(1, 3) = 3
• Height of the Binary Tree rooted at A = 3 + 1 = 4
In this example, the binary tree has a height of 4. As we traverse the paths A > C > E > G and A > B, we correctly calculate the height of the binary tree rooted at A using the depth-first search approach.
Python Code to for Calculating the Height of a Binary Tree Using the Depth First Search Approach
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.data = key
def height(root):
if root is None:
return 0 # Height of an empty tree is 0
left_height = height(root.left)
right_height = height(root.right)
return max(left_height, right_height) + 1
# Constructing the binary tree
root = Node('A')
root.left = Node('B')
root.right = Node('C')
root.right.left = Node('D')
root.right.right = Node('E')
root.right.right.right = Node('G')
tree_height = height(root)
print(f"The height of the binary tree is: {tree_height}")
The output
The height of the binary tree is: 4
Hope you this post helps you to understand how to calculate the diameter of binary tree with Python. Keep in mind CWAssignments provides 24/7 programming homework help for students around the world, so you can get instant python assignment help from experienced programmers in a few clicks.